While sitting in Math Department Chair Erika Amaya’s pre-calculus class, sophomore Iman Mohammed stared blank faced at the whiteboard as Amaya found polynomials with irrational conjugate roots.
After that hour-long class period, Mohammed recalls walking out of class thinking, “‘What did I do? I think I broke math.'”
Earlier that period, the multi-step problem-solving process seemed to be daunting and cumbersome to her. “There has to be a faster way to do this. I don’t want to do all of this work,” she thought.
She wanted to do something different and found a way to find polynomials with irrational conjugate roots without going through the “FOIL-ing” process— the traditional method taught in school.
“I got it done in less than half the time that it would usually take me to do. I showed Ms. Amaya when I did my first step and she said, ‘Um no.’ But then at the end I said, ‘Ms. Amaya, I got the same answer as you did,'” Mohammed said.
After showing Amaya her problem-solving process, Mohammed recalls Amaya saying, “‘Iman, I think you’re onto something. I think you figured something out. I’ve never seen that in math before.'”
She went to math teacher Andy Callender’s room during her free period to do a proof of her method. Although it took “forever,” the two found that it works with all numbers of second-degree polynomials with irrational roots.
Mohammed plans to publish her method and is in the process of doing so. She has requested that The Oracle not share the method at this time in order to protect her intellectual property.
Anyone can watch the video below to see Mohammed use the traditional method of solving polynomials with irrational roots, but for now, Archer students will have to learn about her new method in person.
Sophomore Iman Mohammed uses traditional method of solving polynomials with irrational conjugate roots from Oracle on Vimeo.



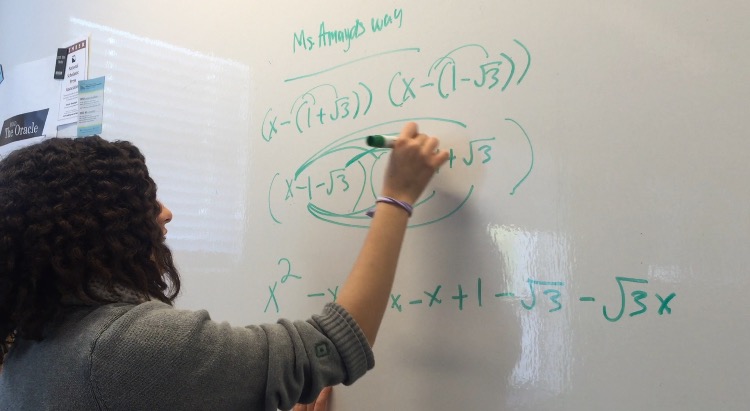
![Faculty and students play in the Color Clash rematch March 20. Danilka Foranda-Zanipatin ('25) plays for the senior team. “Just to have some time deticated to just being supported by [a] large community… it’s just nice to have a little distraction.”](https://archeroracle.org/wp-content/uploads/2025/03/Screenshot-2025-03-20-at-4.12.21 PM.png)





